ある一点から、光が(双方向に)放出される。この点をXとする。同時に、高速の半分の速さで物体が動き始める。この時、光と物体の位置関係をグラフで表すと以下のようになるはずだ。
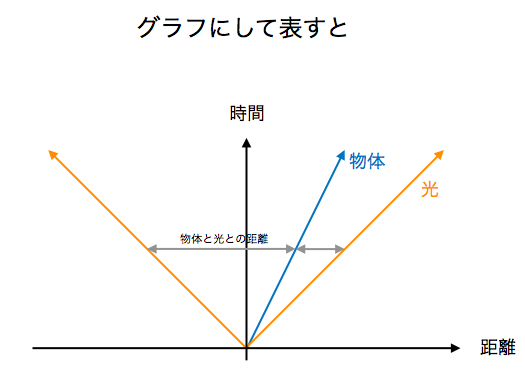
ここで、物体とそれぞれの光の距離は、グレーの矢印の長さになるはずだ。すなわち、物体を視点にして見ると、放出された光と物体との位置関係は(光の速度が一定であるとするならば)以下のようになるはずだ。なぜなら、ある物体と反対方向に自分が動いていた時、自分が止まっている時よりも速く物体は遠ざかっていくからである。
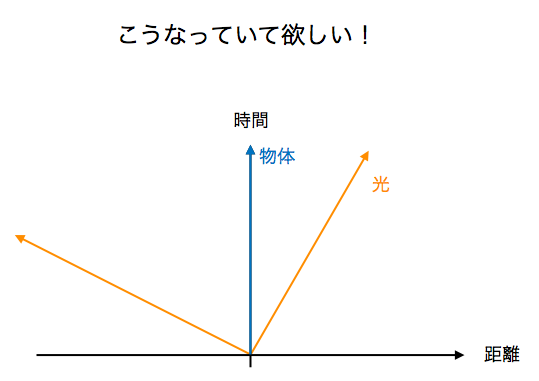
しかし、実際には放出された光の見え方は、自分がどれだけ早く動いていても、同じなのである。光の中心が、勝手についてくるのである。
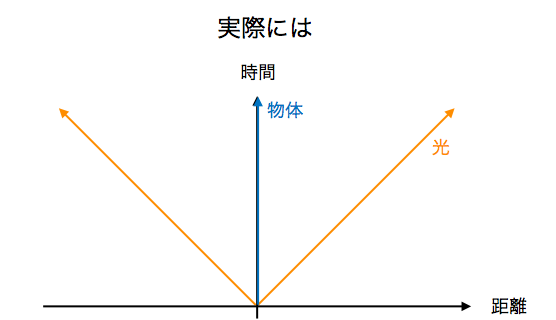
これは一体どうしてだろう?光の(本来の)速さが、見る人によって違うのだろうか?それとも、時空間がねじれているのだろうか?
光の(本来の)速さが、見る人によって違うとすると、これはかなり不都合である。同様に、空間がねじれていると考えるのも、同じ物体が別の場所に存在してしまうことになり、受け入れがたい。
相対性理論では、この問題を、点Xと物体とでは、時間の流れ方が違うと解釈する。だから、点Xにおける時間・空間を、物体における時間・空間に置き換える関数(変換)が必要だ。
そうした時に、「比」を保存するのが大変都合の良いことだとわかる。つまり、最初の図で表した二つのグレーの矢印が、同じ長さであるような軸を取ってやれば、点Xでの話を物体での話に翻訳することが可能だろう。
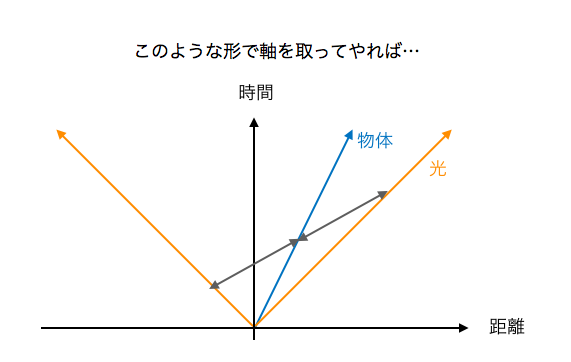
この図におけるグレーの矢印を並行移動したものすべてについて、比が保存される。グレーの矢印上の点全てが、物体にとっては同じ時間に存在することになる。これで、一つの軸は設定し終えた。
もう一つの軸については、ほとんど自明であるが、これは図の中の青い矢印と一致する。そうでなければ、「青矢印上の点」と「物体」との距離が0にならないからだ。「空間は歪ませない」という方針に則るならば、これは青い矢印と一致しなければならない。
二つの軸を設定し終えたところで、それぞれの傾きを求める。まずは青い矢印の軸だが、これは距離=速さ*時間、すなわち$ x = vt $の式から、即座に$ \frac{1}{v} $だとわかる。次に、グレーの軸だが、これは例えばその直線の方程式を$y = ax + b$などと置いて、x成分が同じであることを利用して式を立ててやれば、$\frac{v}{c^2}$($c$は光速)だとわかる。
次に我々がするのは、点Xでの座標系の基底$\hat{i}$と$\hat{j}$で表されていた点を、傾き$\frac{1}{v}$の基底$\hat{i^\prime}$と傾き$\frac{v}{c^2}$の基底$\hat{j^\prime}$で表した時に、各係数の関係を調べることである。
つまり、$x\hat{i}+t\hat{j}=x^\prime\hat{i^\prime}+t^\prime\hat{j^\prime}$の時に、$x^\prime$と$t^\prime$を$x$と$t$で表せば、点Xの座標系を物体の座標系に移す(変換する)ことができる。
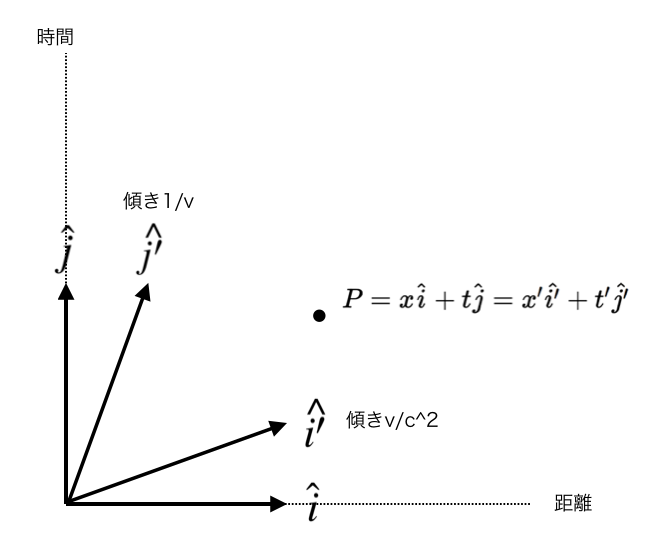
そこで一つ疑問が浮かぶ。$\hat{i^\prime}$と$\hat{j^\prime}$の大きさはどうすれば良いのだろうか?ひとまず、$\hat{i}$から垂線を伸ばし、ぶつかったところを$\hat{i^\prime}$の終点とする。すなわち、$\hat{i}$が$\hat{i^\prime}$の距離軸に対する正射影になるようにする。同様に$\hat{j^\prime}$も決める。そうした上で、$\hat{i^\prime}$と$\hat{j^\prime}$がなす平行四辺形の面積Sを求める。
これは、$\hat{i}$と$\hat{j}$がなす平行四辺形の面積が1であることを考えると、1に合わせておいた方が良い。だから、$\gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$倍する。すなわち、
と定める。こうすると、$ S = 1 $になる。
最後に、$\vec{p}=x\hat{i}+t\hat{j}=x^\prime\hat{i^\prime}+t^\prime\hat{j^\prime}$より、$(x, t)$から$(x^\prime, t^\prime)$への変換を求める。
こうして、ローレンツ変換の公式 $x^\prime = \gamma(x-vt), t^\prime = \gamma(t-\frac{v}{c^2}x)$ が得られた。